経験的直交関数(EOF)展開による欅坂/けやき坂46メンバーの学力パターンの分析

目次

• 概要
• 欅坂46に対する解析
• けやき坂46に対する解析
• 欅坂46とけやき坂46の混合解析

概要

気象学・気候学のデータ解析で広く用いられる手法である経験的直交関数(EOF)展開を，アイドルグループ欅坂46(現 櫻坂46)とけやき坂46(現 日向坂46)の冠テレビ番組内で行われた学力テストの結果に適用し，教科間の得点パターンのメンバーによる違いにおいて卓越するモードを抽出した。番組内で示された得点を教科ごとに規格化し，さらに合計得点に対するトレンドを除去した上でEOFの計算を行った。

テストは欅坂46とけやき坂46とで異なる時期に異なる問題を用いて行われたため，まず欅坂46に対する解析の結果を示し，次にけやき坂46に対する解析の結果を示す。そして，最後にこれらを一つに統合して行った欅坂46とけやき坂46の混合解析の結果を示す。

(遊びでやった解析なので真に受けないこと。長いので，時間のない方は「欅坂46とけやき坂46の混合解析」だけ読めば良いと思う。。。)

欅坂46に対する解析では，EOF1として国語・数学が得意で社会・理科が苦手であるような「国数偏重モード」が，EOF2として国語・社会・英語が得意で，数学・理科が苦手であるような「文系―理系モード」が抽出された(図2，図3)。また，けやき坂46に対する解析では，EOF1として国語・社会・英語が得意で，数学・理科が苦手であるような「文系―理系モード」が，EOF2として英語が得意で社会が苦手であるような「社会―英語偏重モード」抽出された(図5，図6)。欅坂46とけやき坂46との両方で，文系―理系モードのような一般的にイメージしやすいパターンが抽出されたことは興味深い。

それぞれのグループで受験者数は20名程度であり，特に極端な教科間得点分散をもつメンバーが存在する場合には，適切なEOFを得ることが難しいと考えられる。そこで，規格化得点に基づいて両グループの得点を一つに統合し，グループ混合学力順位を作成した(表7)。このようにしてサンプル数を40に増やし，さらに極端な教科間得点分散をもつメンバー数名を除いてEOFを計算した結果，国語と理科のどちらが得意かという指標(EOF1)と社会と数学のどちらが得意かという指標(EOF2)によって，全分散のうち62％が説明できることがわかった(図7，図8，図9)。また，これらのEOFを適当に回転させることによって，国語・社会が得意で数学・理科が苦手な「文系―理系モード」と，国語・数学が得意で社会・理科が苦手な「基盤―応用モード」とに指標を置き換えることができた(図10，図11)。この二つの指標に基づいて欅坂/けやき坂46のメンバー40名を9通りの学力タイプに分類した(表8)。

欅坂46に対する解析

2016年4月10，17日深夜に放送された欅坂46(通称：漢字欅)の冠番組「欅って書けない？」(テレビ東京)にて，5教科(国語・数学・社会・理科・英語)からなる学力テストのメンバーごとの得点が明らかになった。

まず，各メンバーの得点を以下の表1に示す。

表1：欅坂46メンバーの学力テスト結果

		国語	数学	社会	理科	英語	合計
1	長濱ねる	15	20	16	18	20	89
2	米谷奈々未	12	18	18	20	20	88
3	原田葵	12	20	16	20	19	87
4	織田奈那	11	19	9	18	16	73
5	長沢菜々香	8	16	10	18	13	65
6	佐藤詩織	8	10	12	12	19	61
7	守屋茜	8	14	10	17	11	60
8	小林由依	7	10	10	14	14	55
9	小池美波	7	14	8	12	13	54
9	齋藤冬優花	8	12	6	12	16	54
11	尾関梨香	8	16	8	8	13	53
11	菅井友香	11	10	6	9	17	53
13	鈴本美愉	7	12	8	10	11	48
13	平手友梨奈	10	12	6	10	10	48
15	渡邉理佐	6	10	7	16	8	47
16	上村莉菜	13	12	0	12	8	45
17	渡辺梨加	9	9	9	8	6	41
18	土生瑞穂	6	8	4	8	11	37
19	志田愛佳	4	4	7	12	8	35
20	今泉佑唯	6	6	4	6	6	28
21	石森虹花	5	5	4	2	5	21
平均		8.62	12.24	8.48	12.48	12.57	54.38
標準偏差		2.84	4.70	4.35	4.88	4.79	18.47

EOF展開を行う前に，この得点に対して前処理を行う。なぜなら，合計得点が高いほど各教科の得点も高くなる傾向にあるため，この得点からそのままEOFを計算しても，全教科で正(あるいは負)の得点となるパターンをもち，対応するスコアが合計得点の高いメンバーほど大きくなる(あるいは小さくなる)変動が卓越モードとして得られることが自明だからである。今回は，各メンバーの得点そのものではなく教科間の得点パターンに着目したいため，各教科の得点から合計得点に対する線形トレンドを除去する。これは気象学・気候学で行われるEOF解析の前処理において，領域一様に近い昇温パターンを伴う温暖化傾向を，時間に対する線形トレンドの除去によって取り除くこととよく似ている。また，教科間で平均点や標準偏差が異なるため，合計得点に対してある特定の教科が影響しやすいことがあり得る。そのような場合に単にトレンドを除去すると，抽出したいはずのパターンも一部除去されてしまう可能性がある。そこで，この解析では，はじめに各教科の得点を平均0，標準偏差1に規格化し，規格化総合得点を規格化した得点の和として定義する。このようにして得られた得点が以下の表2である。なお，規格化総合得点に基づくと順位の入れ替わりが生じるが，ここでは順位の入れ替えは行わない。後のグループ混合解析では入れ替えた順位を示している(表7)。

表2：欅坂46メンバーの学力テスト結果(規格化後)

		国語	数学	社会	理科	英語	総合
1	長濱ねる	2.25	1.65	1.73	1.13	1.55	8.31
2	米谷奈々未	1.19	1.23	2.19	1.54	1.55	7.70
3	原田葵	1.19	1.65	1.73	1.54	1.34	7.45
4	織田奈那	0.84	1.44	0.12	1.13	0.72	4.25
5	長沢菜々香	-0.22	0.80	0.35	1.13	0.09	2.15
6	佐藤詩織	-0.22	-0.48	0.81	-0.10	1.34	1.35
7	守屋茜	-0.22	0.37	0.35	0.93	-0.33	1.10
8	小林由依	-0.57	-0.48	0.35	0.31	0.30	-0.09
9	小池美波	-0.57	0.37	-0.11	-0.10	0.09	-0.32
9	齋藤冬優花	-0.22	-0.05	-0.57	-0.10	0.72	-0.22
11	尾関梨香	-0.22	0.80	-0.11	-0.92	0.09	-0.36
11	菅井友香	0.84	-0.48	-0.57	-0.71	0.92	0.00
13	鈴本美愉	-0.57	-0.05	-0.11	-0.51	-0.33	-1.57
13	平手友梨奈	0.49	-0.05	-0.57	-0.51	-0.54	-1.18
15	渡邉理佐	-0.92	-0.48	-0.34	0.72	-0.95	-1.97
16	上村莉菜	1.54	-0.05	-1.95	-0.10	-0.95	-1.51
17	渡辺梨加	0.13	-0.69	0.12	-0.92	-1.37	-2.73
18	土生瑞穂	-0.92	-0.90	-1.03	-0.92	-0.33	-4.10
19	志田愛佳	-1.63	-1.75	-0.34	-0.10	-0.95	-4.77
20	今泉佑唯	-0.92	-1.33	-1.03	-1.33	-1.37	-5.98
21	石森虹花	-1.28	-1.54	-1.03	-2.14	-1.58	-7.57
平均		0.00	0.00	0.00	0.00	0.00	0.00
標準偏差		1.00	1.00	1.00	1.00	1.00	4.24

規格化総合得点は，規格化前の合計得点と比べて，標準偏差の小さな国語からの寄与がより大きくなる。そのため，規格化前に1点差ずつ離れていた上位3名について規格化総合得点でみると，国語の得点が高かった1位の長濱ねるが下位2名をより離す形で1位となっている。11位の菅井友香が8位の小林由依より上位となっているのも，標準偏差が小さく合計得点に影響しにくい国語の点数が相対的に高かったことが効いていると考えられる。

次に，各教科の得点から規格化総合得点に対するトレンドを除去する。各メンバーの得点は表3のようになる。

表3：欅坂46メンバーの学力テスト結果(規格化・トレンド除去後)

		国語	数学	社会	理科	英語
1	長濱ねる	0.73	-0.14	0.09	-0.54	-0.15
2	米谷奈々未	-0.22	-0.43	0.67	0.00	-0.02
3	原田葵	-0.17	0.05	0.26	0.04	-0.18
4	織田奈那	0.06	0.53	-0.72	0.28	-0.15
5	長沢菜々香	-0.61	0.34	-0.07	0.70	-0.35
6	佐藤詩織	-0.47	-0.77	0.54	-0.37	1.06
7	守屋茜	-0.42	0.14	0.13	0.70	-0.55
8	小林由依	-0.55	-0.46	0.37	0.33	0.32
9	小池美波	-0.51	0.44	-0.05	-0.03	0.15
9	齋藤冬優花	-0.18	0.00	-0.53	-0.05	0.76
11	尾関梨香	-0.15	0.88	-0.04	-0.85	0.16
11	菅井友香	0.84	-0.48	-0.57	-0.71	0.92
13	鈴本美愉	-0.28	0.29	0.20	-0.19	-0.01
13	平手友梨奈	0.70	0.20	-0.34	-0.27	-0.30
15	渡邉理佐	-0.56	-0.05	0.05	1.12	-0.55
16	上村莉菜	1.82	0.27	-1.65	0.20	-0.65
17	渡辺梨加	0.63	-0.10	0.66	-0.37	-0.82
18	土生瑞穂	-0.17	-0.02	-0.22	-0.09	0.51
19	志田愛佳	-0.76	-0.73	0.60	0.86	0.02
20	今泉佑唯	0.17	-0.04	0.15	-0.13	-0.15
21	石森虹花	0.11	0.09	0.46	-0.63	-0.03

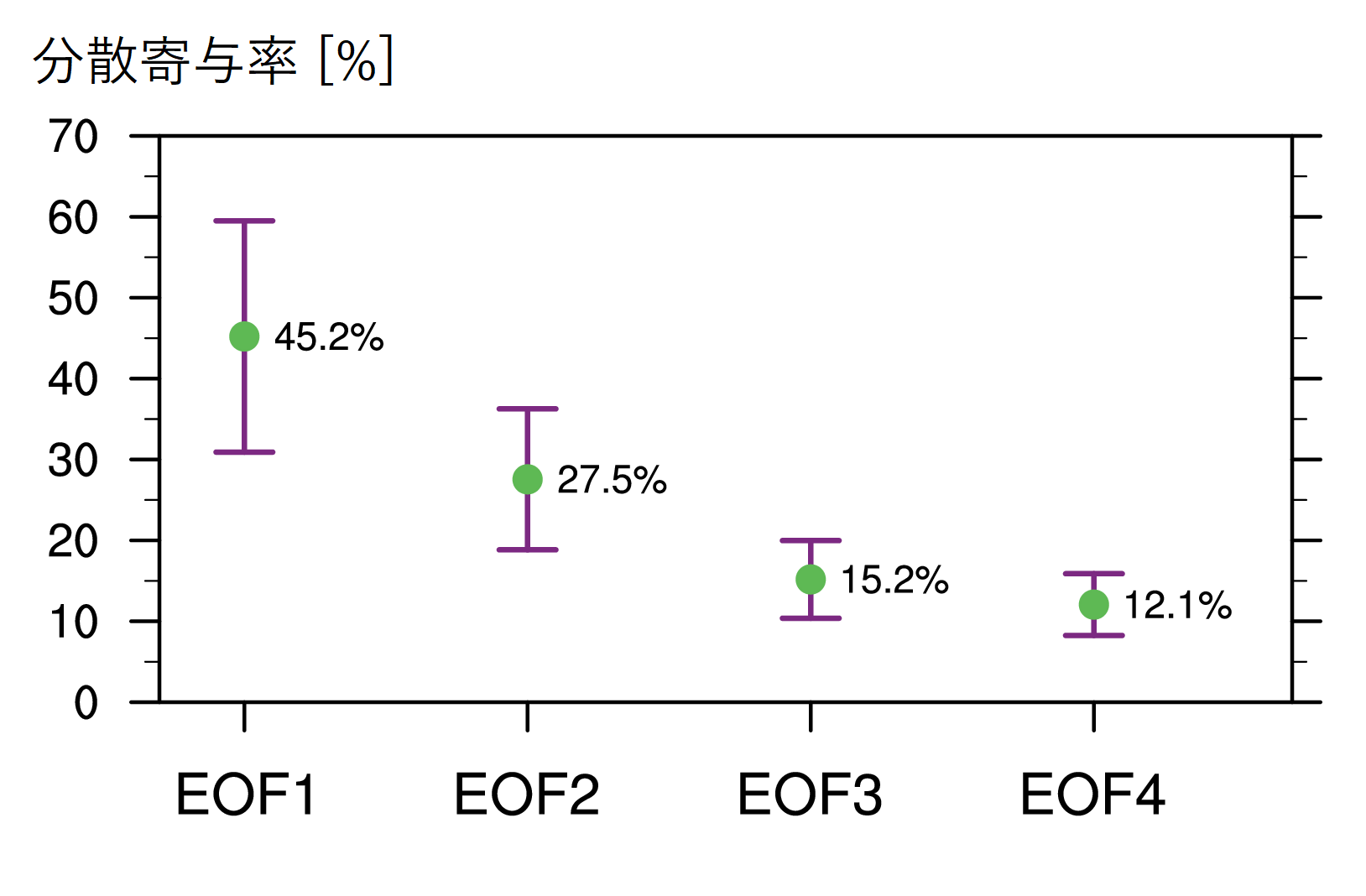
さて，この得点に基づいて分散行列を定義し，EOF解析を行う。得られた各モードの分散寄与率を図1に示す。エラーバーはNorth et al. (1982)の式(24)に基づく。第1モード(EOF1)が45.2％，第2モード(EOF2)が27.5％，第3モード(EOF3)が15.2％，第4モード(EOF4)が12.1％となった。一般に，EOF展開において分散寄与率の近いモードは別々に分離したモードであると考えることができず，分散寄与率が近いベクトル同士の任意の線形結合が可能であると解釈すべきだとされている。図1中のエラーバーで示されたNorthの基準に従えば，これらのEOFは分離していないと解釈すべきなのかもしれない。しかし，ここでは少し甘く見て，EOF1とEOF2を分離したモードとして議論を進める。EOF3とEOF4は分散寄与率が低く，分離もさらに悪くなるためにここでは用いない。そもそも数学的に4つしかありえないEOFうち3番目や4番目のモードに意味をもたせることがナンセンスであって，それだとEOF解析を行う意味がない。なお，EOF1とEOF2だけで全分散の70％以上(約72.7％)を説明することができる。

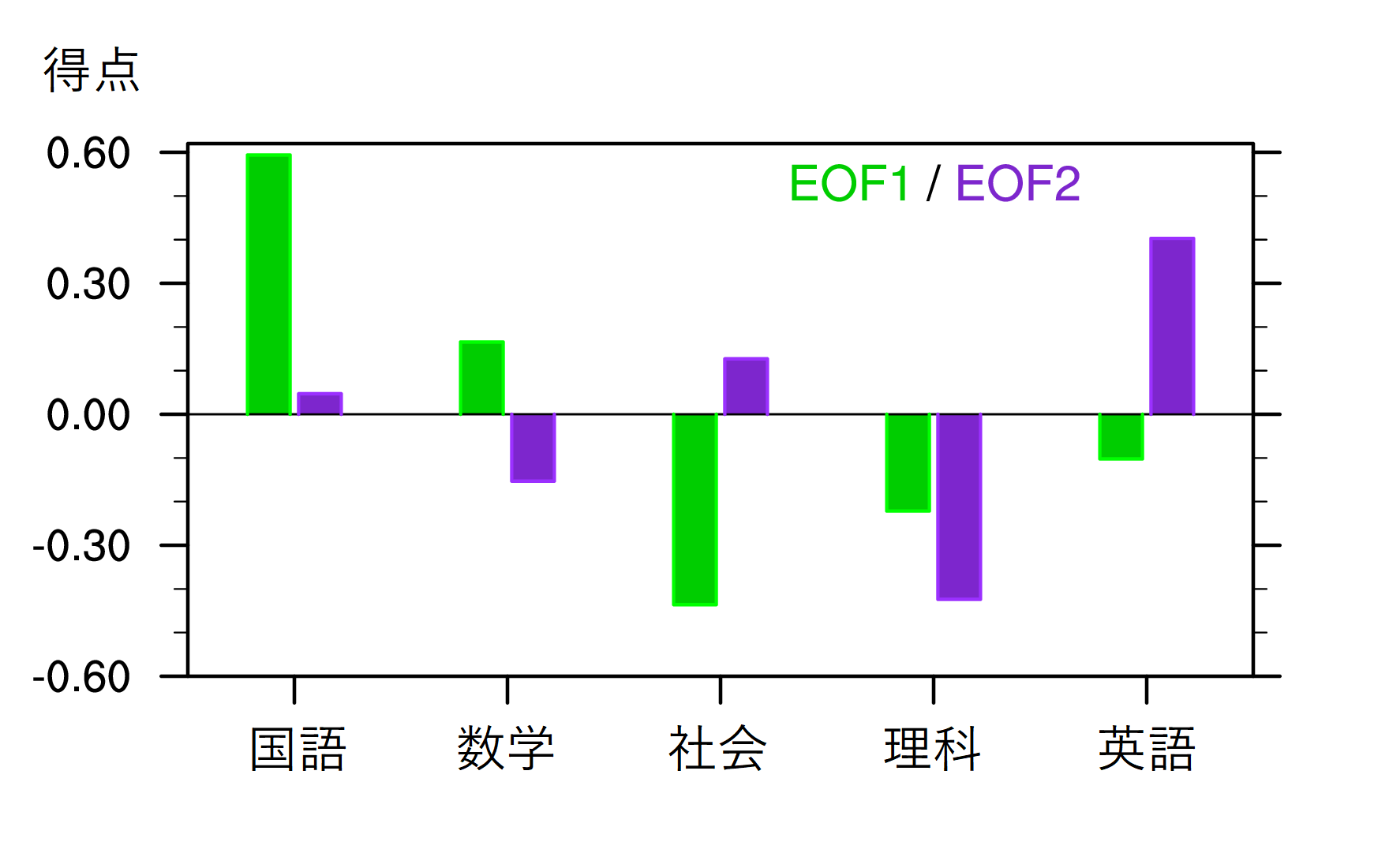
次に，EOF1とEOF2の得点パターン(図2)をみる。EOF1は，大雑把に言えば，国語と数学で得点が高く，社会と理科で得点が低い傾向を示す。そこで，このEOF1を「国数偏重モード」と名づけよう。また，EOF2は，大雑把に言えば，国語・社会・英語で得点が高く，数学と理科で得点が低い傾向を示すパターンをもつ。そこで，このEOF2を「文系―理系モード」と名づけよう。なお，このようなモードに名前をつける行為は，話を分かりやすくすると同時に誤解を生みやすくするので注意が必要である。例えば，今回のEOF2について考えると，たまたま図2のEOF2のような得点分布が世間の文系―理系のイメージに比較的近かったので，EOF2という無機質な名称よりは良かろうという考えで，このような名前をつけただけである。決して，一般的に文系―理系を表すパターンがこれであると主張したいわけではない。また，EOF解析で抽出されるモードは，あくまでも固有値や固有ベクトルとして数学的に求まるものであり，そこに物理的な意味があるかどうかは分からないことにも注意が必要である。研究で使う際にはこれらを認識した上で用いなくてはならないし，単にEOFを計算するだけでは研究にはならない。つまり，何が言いたいかというと，このコラムは研究ではないので，その点は大目に見てほしいということである。

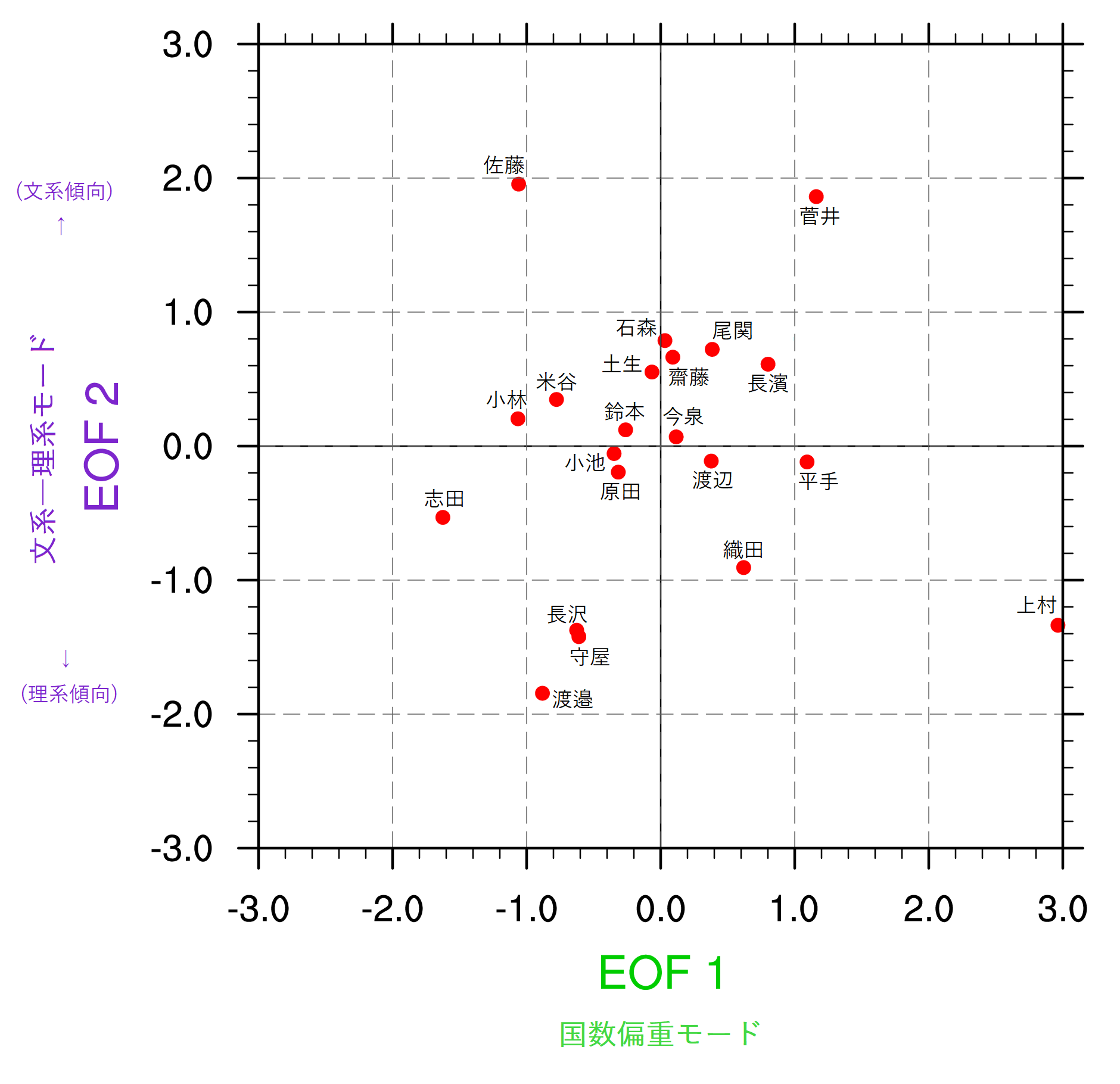
各メンバーの「国数偏重モード」のスコアを横軸に「文系―理系モード」のスコアを縦軸にプロットすると図3のようになる。グラフの右側に位置するメンバーほど国語と数学で点数を稼ぐ傾向にあり，上村莉菜・平手友梨奈・長濱ねるがその代表例である。一方，グラフの左側に位置するメンバーほど社会と理科で点数を稼ぐ傾向にあり，志田愛佳・小林由依・米谷奈々未がその代表例である。また，グラフの上側に位置するメンバーほど文系傾向にあり，佐藤詩織・菅井友香がその代表例である。一方，グラフの下側に位置するメンバーほど理系傾向にあり，渡邉理佐・守屋茜・長沢菜々香・織田奈那がその代表例である。

ところで，図3を見ると，上村莉菜が集団から外れた位置にあることが分かる。これは，社会が0点にもかかわらず他でそこそこの点数を取ったためと考えられる。ここでは示さないが，上村莉菜を除いて計算するとEOFのパターンが変わる。サンプル数が少ないほどこのような外れ値(ここでは極端な分散をもつサンプル)に結果が影響されやすい。後で，欅坂46とけやき坂46の混合解析を行う際には，上村莉菜を除いたメンバーでEOFの計算を行っている。

けやき坂46に対する解析

2018年9月9，16日深夜に放送されたけやき坂46(通称：ひらがなけやき)の冠番組「ひらがな推し」(テレビ東京)においても，同様の試験が行われ，けやき坂46メンバーの得点も明らかになった。そこで，これに対しても同じ解析を行った。まず，各メンバーの得点は以下の表4の通りである。

表4：けやき坂46メンバーの学力テスト結果

		国語	数学	社会	理科	英語	合計
1	宮田愛萌	16	18	13	12	12	71
2	佐々木久美	10	17	13	12	14	66
3	高瀬愛奈	7	18	9	14	17	65
4	金村美玖	8	18	9	14	12	61
5	松田好花	6	19	8	13	14	60
6	渡邉美穂	9	16	10	12	12	59
7	丹生明里	4	17	8	11	12	52
8	潮紗理菜	7	14	7	9	12	49
9	柿崎芽実	6	12	6	11	9	44
10	富田鈴花	6	6	8	11	10	41
11	河田陽菜	3	12	5	11	5	36
11	小坂菜緒	2	11	9	9	5	36
13	加藤史帆	1	14	7	5	5	32
14	井口眞緒	4	7	5	5	5	26
15	東村芽依	1	8	6	4	6	25
16	佐々木美玲	1	11	3	6	2	23
17	高本彩花	0	5	7	8	1	21
18	齊藤京子	3	3	1	1	8	16
19	濱岸ひより	0	5	0	6	0	11
平均		4.95	12.16	7.05	9.16	8.47	41.79
標準偏差		4.08	5.21	3.39	3.72	4.85	18.60

これに対して，先ほどと同様の前処理を行う。各教科の得点の平均を0，標準偏差を1に揃え，それらの和を規格化総合得点としたものが次の表5である。

表5：けやき坂46メンバーの学力テスト結果(規格化後)

		国語	数学	社会	理科	英語	総合
1	宮田愛萌	2.71	1.12	1.75	0.76	0.73	7.07
2	佐々木久美	1.24	0.93	1.75	0.76	1.14	5.82
3	高瀬愛奈	0.50	1.12	0.57	1.30	1.76	5.25
4	金村美玖	0.75	1.12	0.57	1.30	0.73	4.47
5	松田好花	0.26	1.31	0.28	1.03	1.14	4.02
6	渡邉美穂	0.99	0.74	0.87	0.76	0.73	4.09
7	丹生明里	-0.23	0.93	0.28	0.50	0.73	2.21
8	潮紗理菜	0.50	0.35	-0.02	-0.04	0.73	1.52
9	柿崎芽実	0.26	-0.03	-0.31	0.50	0.11	0.53
10	富田鈴花	0.26	-1.18	0.28	0.50	0.31	0.17
11	河田陽菜	-0.48	-0.03	-0.61	0.50	-0.72	-1.34
11	小坂菜緒	-0.72	-0.22	0.57	-0.04	-0.72	-1.13
13	加藤史帆	-0.97	0.35	-0.02	-1.12	-0.72	-2.48
14	井口眞緒	-0.23	-0.99	-0.61	-1.12	-0.72	-3.67
15	東村芽依	-0.97	-0.80	-0.31	-1.39	-0.51	-3.98
16	佐々木美玲	-0.97	-0.22	-1.20	-0.85	-1.34	-4.58
17	高本彩花	-1.21	-1.37	-0.02	-0.31	-1.54	-4.45
18	齊藤京子	-0.48	-1.76	-1.79	-2.20	-0.10	-6.33
19	濱岸ひより	-1.21	-1.37	-2.08	-0.85	-1.75	-7.26
平均		0.00	0.00	0.00	0.00	0.00	0.00
標準偏差		1.00	1.00	1.00	1.00	1.00	4.37

さらに，規格化総合得点に対するトレンドを取り除いた得点を次の表6に示す。

表6：けやき坂46メンバーの学力テスト結果(規格化・トレンド除去後)

		国語	数学	社会	理科	英語
1	宮田愛萌	1.31	-0.31	0.33	-0.64	-0.70
2	佐々木久美	0.08	-0.25	0.59	-0.39	-0.03
3	高瀬愛奈	-0.54	0.06	-0.48	0.26	0.70
4	金村美玖	-0.14	0.22	-0.32	0.41	-0.17
5	松田好花	-0.54	0.50	-0.53	0.23	0.33
6	渡邉美穂	0.18	-0.09	0.05	-0.05	-0.10
7	丹生明里	-0.67	0.49	-0.16	0.06	0.29
8	潮紗理菜	0.20	0.05	-0.32	-0.35	0.42
9	柿崎芽実	0.15	-0.14	-0.42	0.39	0.00
10	富田鈴花	0.23	-1.22	0.25	0.46	0.28
11	河田陽菜	-0.21	0.24	-0.34	0.76	-0.45
11	小坂菜緒	-0.50	0.01	0.80	0.18	-0.49
13	加藤史帆	-0.48	0.85	0.48	-0.63	-0.22
14	井口眞緒	0.49	-0.25	0.13	-0.39	0.02
15	東村芽依	-0.18	0.00	0.49	-0.60	0.29
16	佐々木美玲	-0.06	0.70	-0.28	0.06	-0.42
17	高本彩花	-0.33	-0.47	0.88	0.57	-0.65
18	齊藤京子	0.77	-0.48	-0.52	-0.94	1.17
19	濱岸ひより	0.23	0.09	-0.62	0.59	-0.29

この得点に基づいて分散行列を定義してEOF解析を行った。図1と同様に，ここで得られたEOFの分散寄与率を示したものが図4である。第1モード(EOF1)が36.0％，第2モード(EOF2)が29.0％，第3モード(EOF3)が20.4％，第4モード(EOF4)が14.5％となった。欅坂46に対してのEOFよりも各モードの分離は悪くなったが，ここでもEOF1とEOF2に基づいて議論を進める。

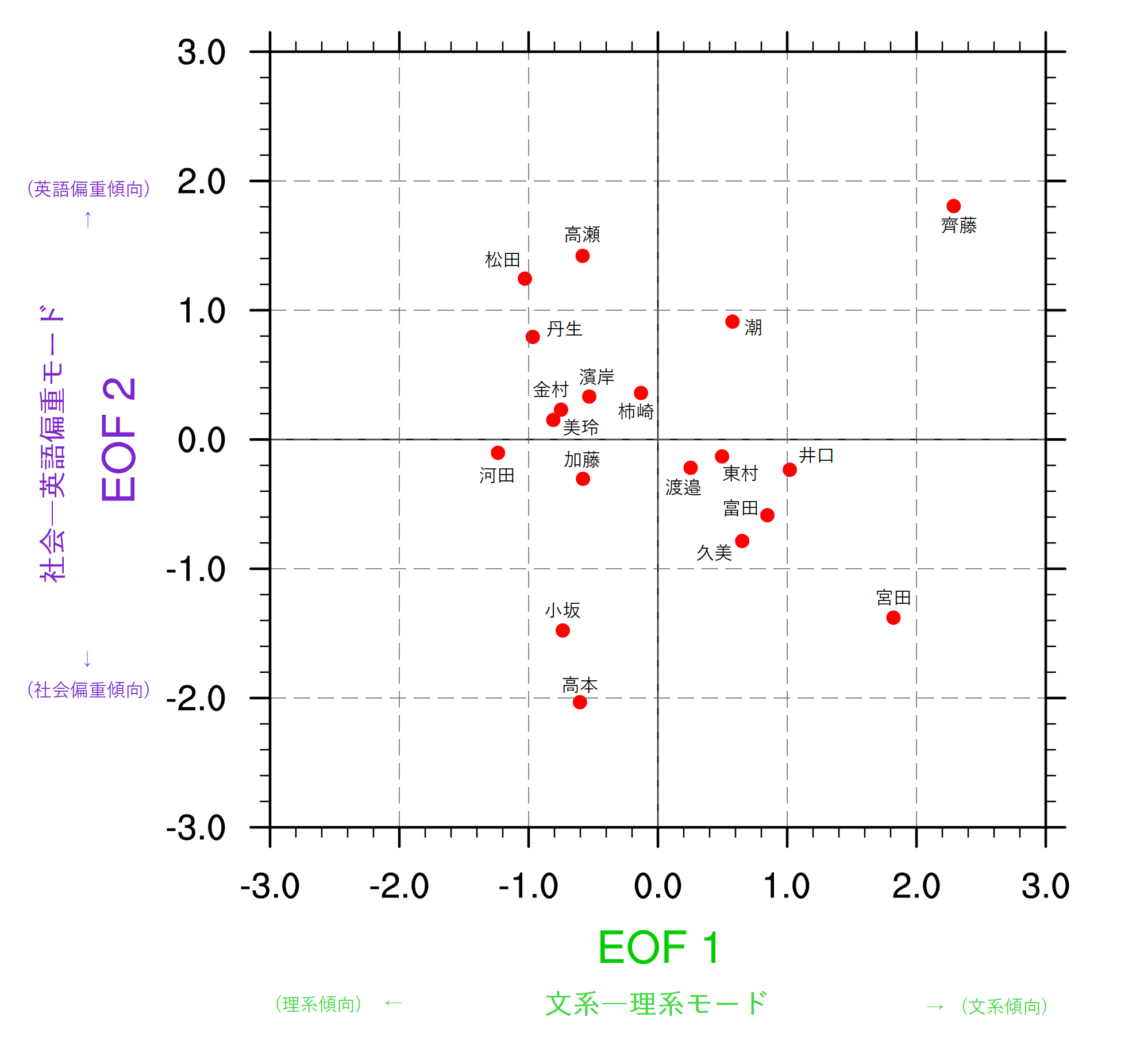
EOF1は，大雑把に言えば，国語・社会・英語で得点が高く数学・理科で得点が低いパターンを示す(図5)。この傾向は欅坂46のEOF2として抽出された「文系―理系モード」とよく似ている(図2)。分散寄与率の順位が異なるとはいえ，「文系―理系モード」がどちらのグループにおいてもEOFとして抽出されることは興味深い。一方，EOF2は，大雑把に言えば，英語で得点が高く社会で得点が低いパターンを示す(図5)。そこで，これを「社会―英語偏重モード」と名付けることにする。

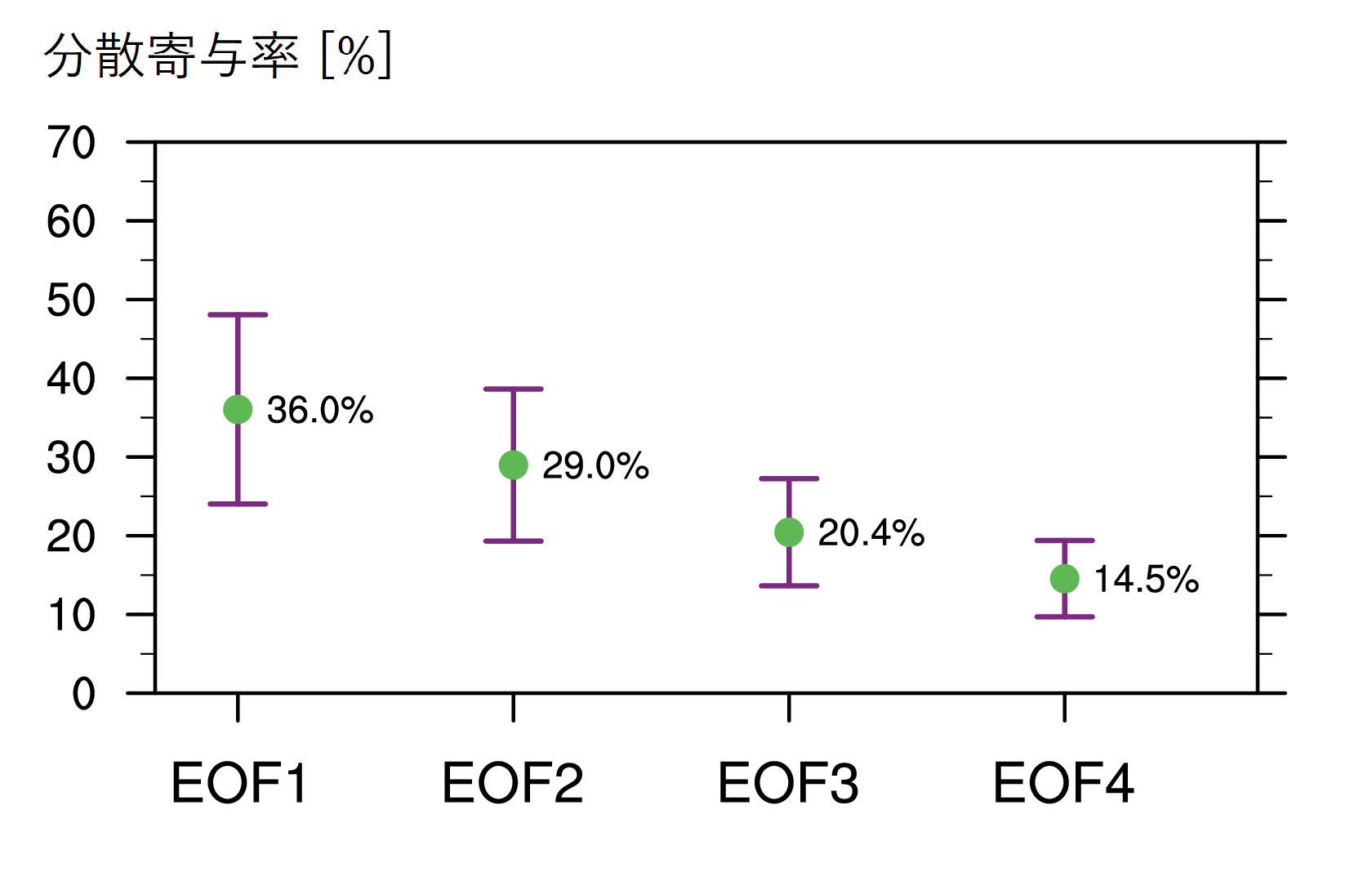
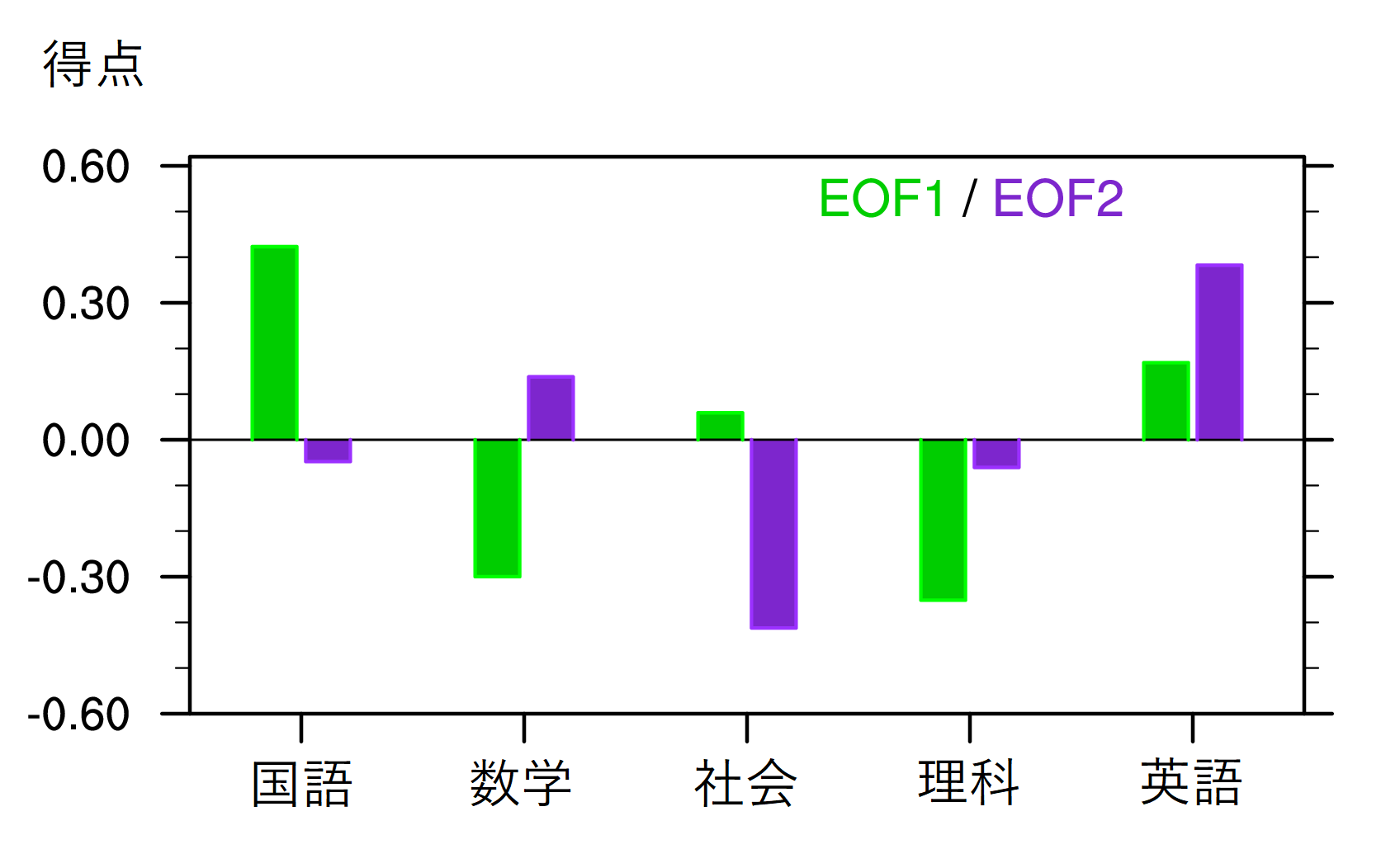
図3にならって，各メンバーの「文系―理系モード」のスコアを横軸に，「社会―英語偏重モード」のスコアを縦軸にプロットすると図6のようになる。グラフの右側に位置するメンバーほど文系傾向にあり，宮田愛萌・齊藤京子・井口眞緒がその代表例である。一方，グラフの左側に位置するメンバーほど理系傾向にあり，河田陽菜・丹生明里がその代表例である。また，グラフの上側に位置するメンバーほど社会と英語で比べると英語で得点を稼ぐ傾向にあり，高瀬愛奈・松田好花・潮紗理菜がその代表例である。一方，グラフの下側に位置するメンバーほど英語よりも社会で得点を稼ぐ傾向にあり，高本彩花・小坂菜緒がその代表例である。欅坂46における上村莉菜がそうであったように，ここでは齊藤京子が外れ値気味である。

欅坂46とけやき坂46の混合解析

欅坂46とけやき坂46とで受けているテストの問題が異なるため，これらを同一視することは好ましくないだろう。しかし，これまでのサンプル数20程度のEOF解析ではサンプリングエラーが大きく，安定したEOFを得ることが難しい。そこで，欅坂とけやき坂を同一視して，サンプル数をおよそ倍にしたEOF解析も試みる。

まず，両グループの規格化得点(表2，表5)を結合させると表7のようになる。ここでは，欅坂46とけやき坂46のグループ混合学力を示すという目的で，規格化総合得点に基づいて改めて順位をつけ直している。

表7：欅坂/けやき坂46の規格化得点に基づくグループ混合学力順位

		国語	数学	社会	理科	英語	総合
1	長濱ねる	2.25	1.65	1.73	1.13	1.55	8.31
2	米谷奈々未	1.19	1.23	2.19	1.54	1.55	7.70
3	原田葵	1.19	1.65	1.73	1.54	1.34	7.45
4	宮田愛萌	2.71	1.12	1.75	0.76	0.73	7.07
5	佐々木久美	1.24	0.93	1.75	0.76	1.14	5.82
6	高瀬愛奈	0.50	1.12	0.57	1.30	1.76	5.25
7	金村美玖	0.75	1.12	0.57	1.30	0.73	4.47
8	織田奈那	0.84	1.44	0.12	1.13	0.72	4.25
9	渡邉美穂	0.99	0.74	0.87	0.76	0.73	4.09
10	松田好花	0.26	1.31	0.28	1.03	1.14	4.02
11	丹生明里	-0.23	0.93	0.28	0.50	0.73	2.21
12	長沢菜々香	-0.22	0.80	0.35	1.13	0.09	2.15
13	潮紗理菜	0.50	0.35	-0.02	-0.04	0.73	1.52
14	佐藤詩織	-0.22	-0.48	0.81	-0.10	1.34	1.35
15	守屋茜	-0.22	0.37	0.35	0.93	-0.33	1.10
16	柿崎芽実	0.26	-0.03	-0.31	0.50	0.11	0.53
17	富田鈴花	0.26	-1.18	0.28	0.50	0.31	0.17
18	菅井友香	0.84	-0.48	-0.57	-0.71	0.92	0.00
19	小林由依	-0.57	-0.48	0.35	0.31	0.30	-0.09
20	齋藤冬優花	-0.22	-0.05	-0.57	-0.10	0.72	-0.22
21	小池美波	-0.57	0.37	-0.11	-0.10	0.09	-0.32
22	尾関梨香	-0.22	0.80	-0.11	-0.92	0.09	-0.36
23	小坂菜緒	-0.72	-0.22	0.57	-0.04	-0.72	-1.13
24	平手友梨奈	0.49	-0.05	-0.57	-0.51	-0.54	-1.18
25	河田陽菜	-0.48	-0.03	-0.61	0.50	-0.72	-1.34
26	上村莉菜	1.54	-0.05	-1.95	-0.10	-0.95	-1.51
27	鈴本美愉	-0.57	-0.05	-0.11	-0.51	-0.33	-1.57
28	渡邉理佐	-0.92	-0.48	-0.34	0.72	-0.95	-1.97
29	加藤史帆	-0.97	0.35	-0.02	-1.12	-0.72	-2.48
30	渡辺梨加	0.13	-0.69	0.12	-0.92	-1.37	-2.73
31	井口眞緒	-0.23	-0.99	-0.61	-1.12	-0.72	-3.67
32	東村芽依	-0.97	-0.80	-0.31	-1.39	-0.51	-3.98
33	土生瑞穂	-0.92	-0.90	-1.03	-0.92	-0.33	-4.10
34	高本彩花	-1.21	-1.37	-0.02	-0.31	-1.54	-4.45
35	佐々木美玲	-0.97	-0.22	-1.20	-0.85	-1.34	-4.58
36	志田愛佳	-1.63	-1.75	-0.34	-0.10	-0.95	-4.77
37	今泉佑唯	-0.92	-1.33	-1.03	-1.33	-1.37	-5.98
38	齊藤京子	-0.48	-1.76	-1.79	-2.20	-0.10	-6.33
39	濱岸ひより	-1.21	-1.37	-2.08	-0.85	-1.75	-7.26
40	石森虹花	-1.28	-1.54	-1.03	-2.14	-1.58	-7.57

さて，この得点をもとにEOFの計算を行いたいが，ここではサンプル数が増えたため，欅坂46のなかで最も外れ値的であった上村莉菜と，けやき坂46のなかで最も外れ値的であった齊藤京子を除いた上でEOFの計算を行う。まず，欅坂46とけやき坂46に対して，それぞれ上村莉菜と齊藤京子を除いたメンバーに対して得点の規格化およびトレンドの除去を行う。その後，それぞれのグループの得点を一つにまとめて分散行列を作成し，EOF展開を行う。EOFの計算から除いた2名のスコアは，この2名を除いて得られた各EOFに対してそれぞれの得点を射影することで求める。恣意的に外れ値であると決めて除くのは適切ではないだろうが，ここでは遊びだと思って大目に見てほしい。

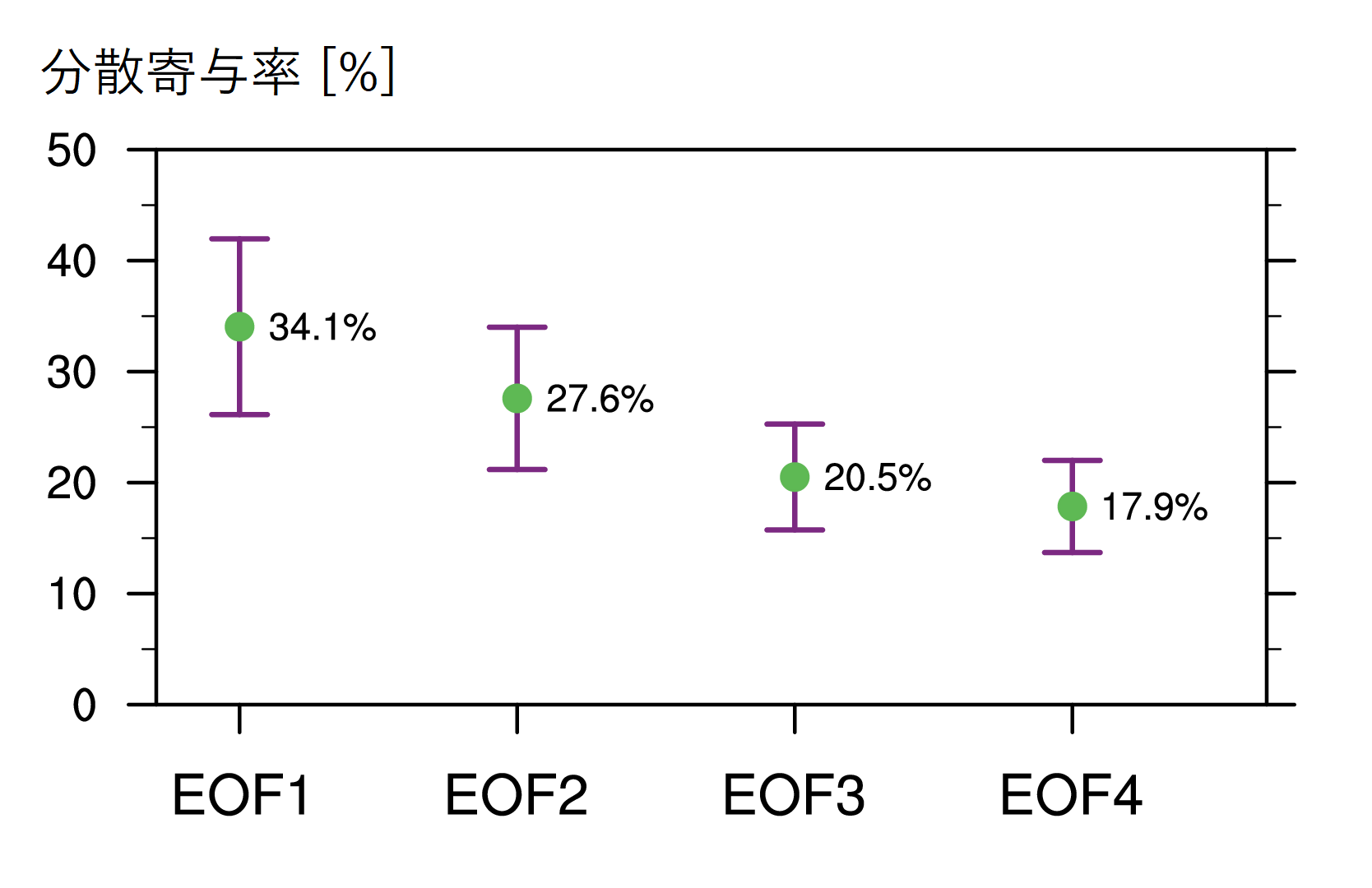
図1や図4と同様に，ここで得られたEOFの分散寄与率を示したものが図7である。第1モード(EOF1)が34.1％，第2モード(EOF2)が27.6％，第3モード(EOF3)が20.5％，第4モード(EOF4)が17.9％となった。相変わらず各モードの分離は悪いが，ここでもまずはEOF1とEOF2を分離したモードであるとして解析を進める。

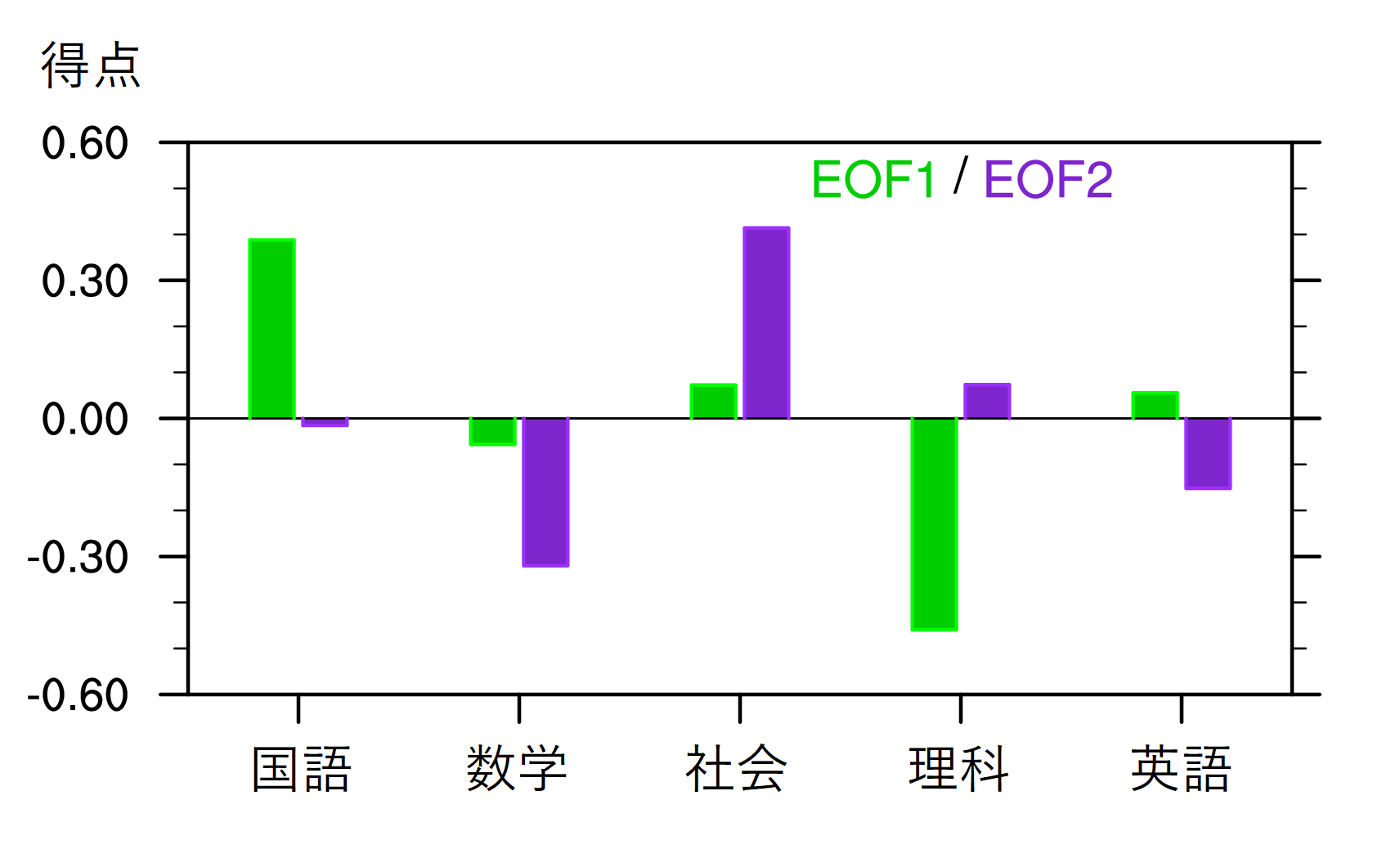
EOF1もEOF2も，基本的には2教科の得点のシーソーによって特徴づけられる(図8)。EOF1は国語で得点が高く，理科で得点が低いパターンを示し，「国語―理科偏重モード」と名付けることにする。一方，EOF2は社会で得点が高く，数学で得点が低いパターンを示し，「社会―数学偏重モード」と名付けることにする。この結果は，各教科間の得点の相関係数のうち絶対値が比較的大きいものが，国語と理科(-0.51)および社会と数学(-0.41)の間の相関係数であったことと整合的である(トレンド除去に伴って各メンバーの合計得点が0となる束縛が課されるため，教科間の得点の相関係数が負になりやすいことに注意)。図3や図6にならって，各メンバーの「国語―理科偏重モード」のスコアを横軸に，「社会―数学偏重モード」のスコアを縦軸にプロットすると図9のようになる。

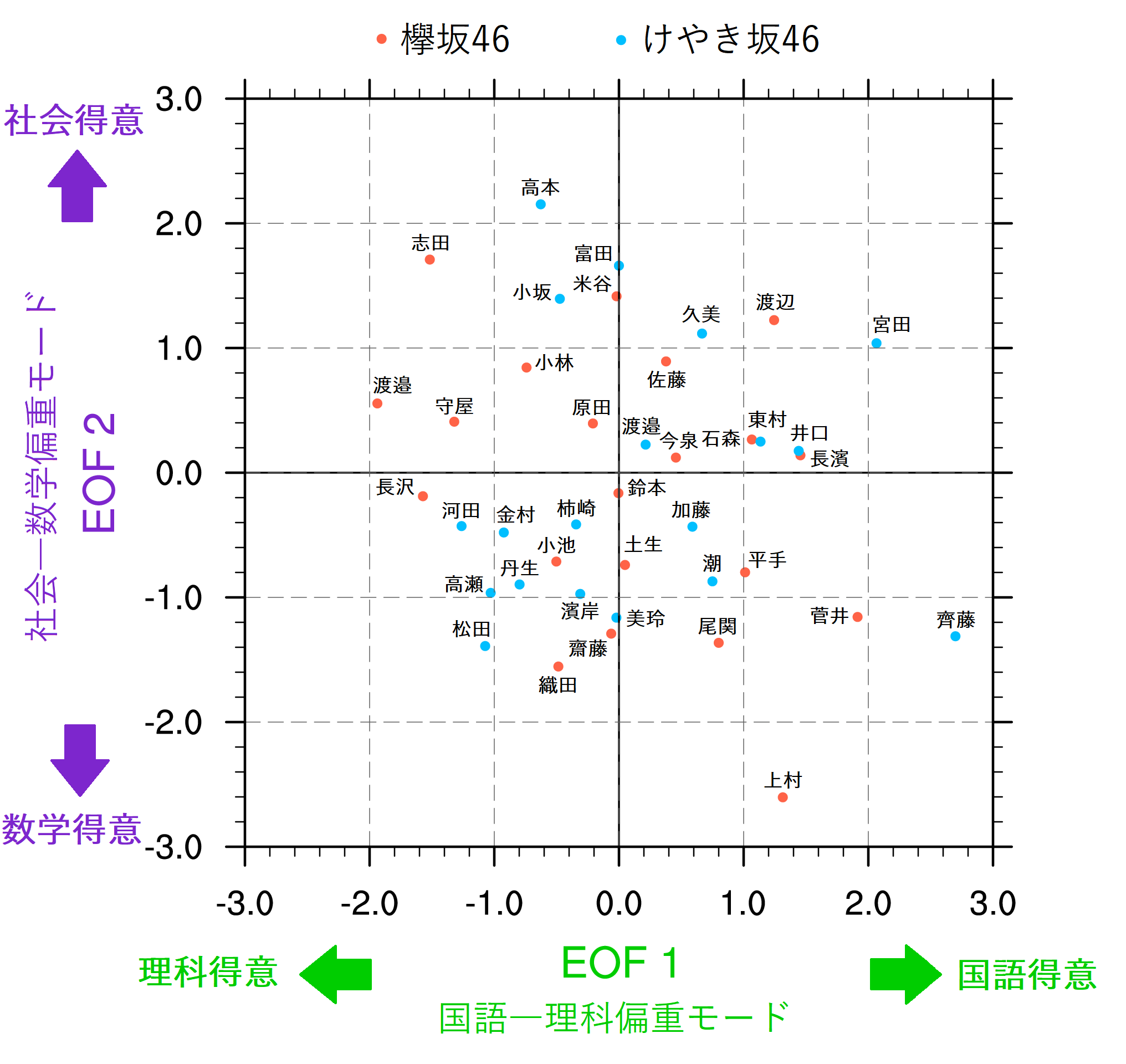
さて，以前の欅坂46に対する解析やけやき坂46に対する解析でEOFとして抽出された「文系―理系モード」がここでは出て来なかった。しかし，図8や図9を眺めると，EOF1＋EOF2が大きいほど(図9の右上ほど)文系傾向をもち，小さいほど(図9の左下ほど)理系傾向をもつことが分かる。そこで，これまでの「文系―理系モード」に近いモードが現れることを期待して，EOF1とEOF2を45度回転させる。もともとEOF1とEOF2の分離がそれほど良くないことから，これらの任意の線形結合が可能であると解釈して，最も解釈のしやすいパターンを恣意的に選ぼうという目論見である。

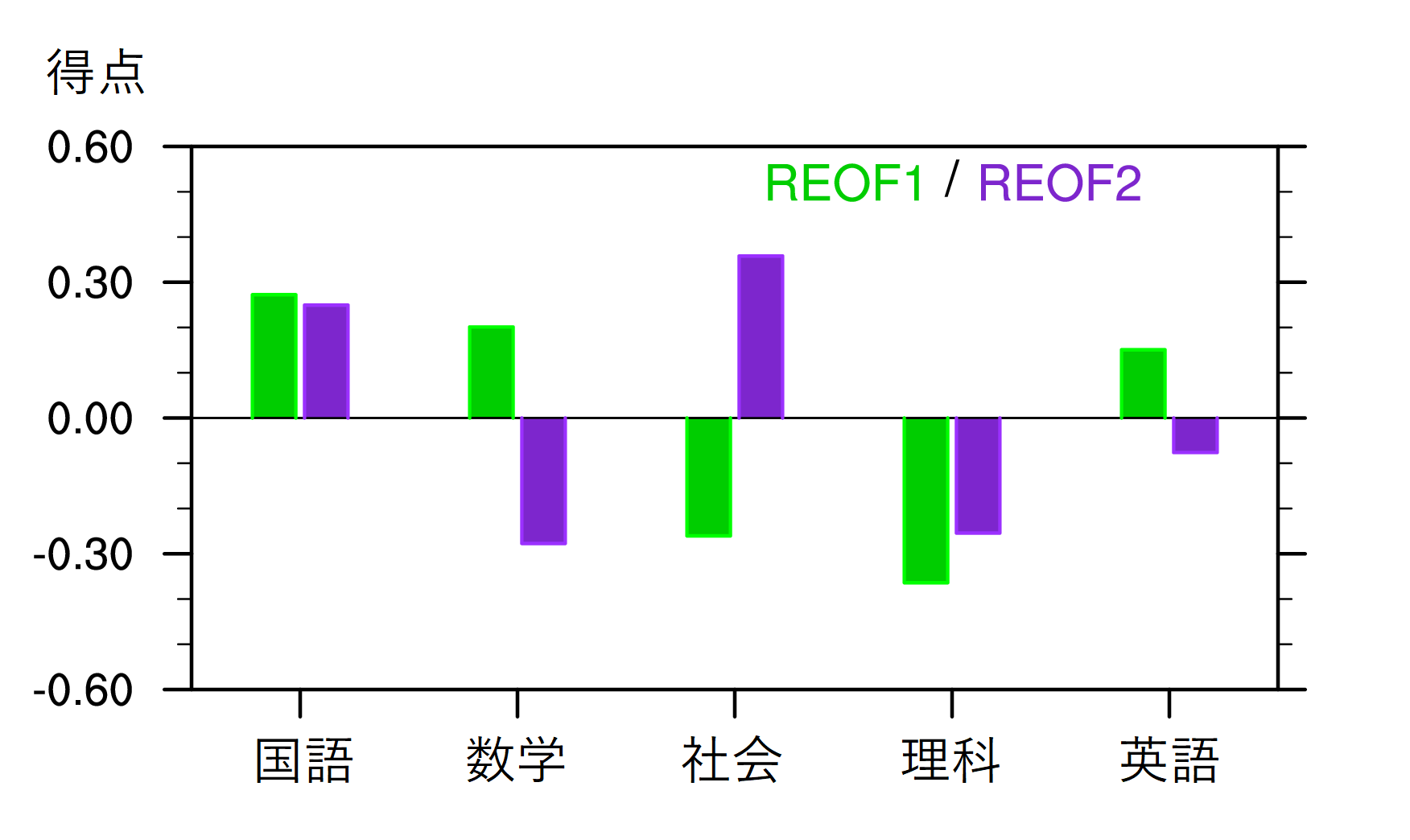
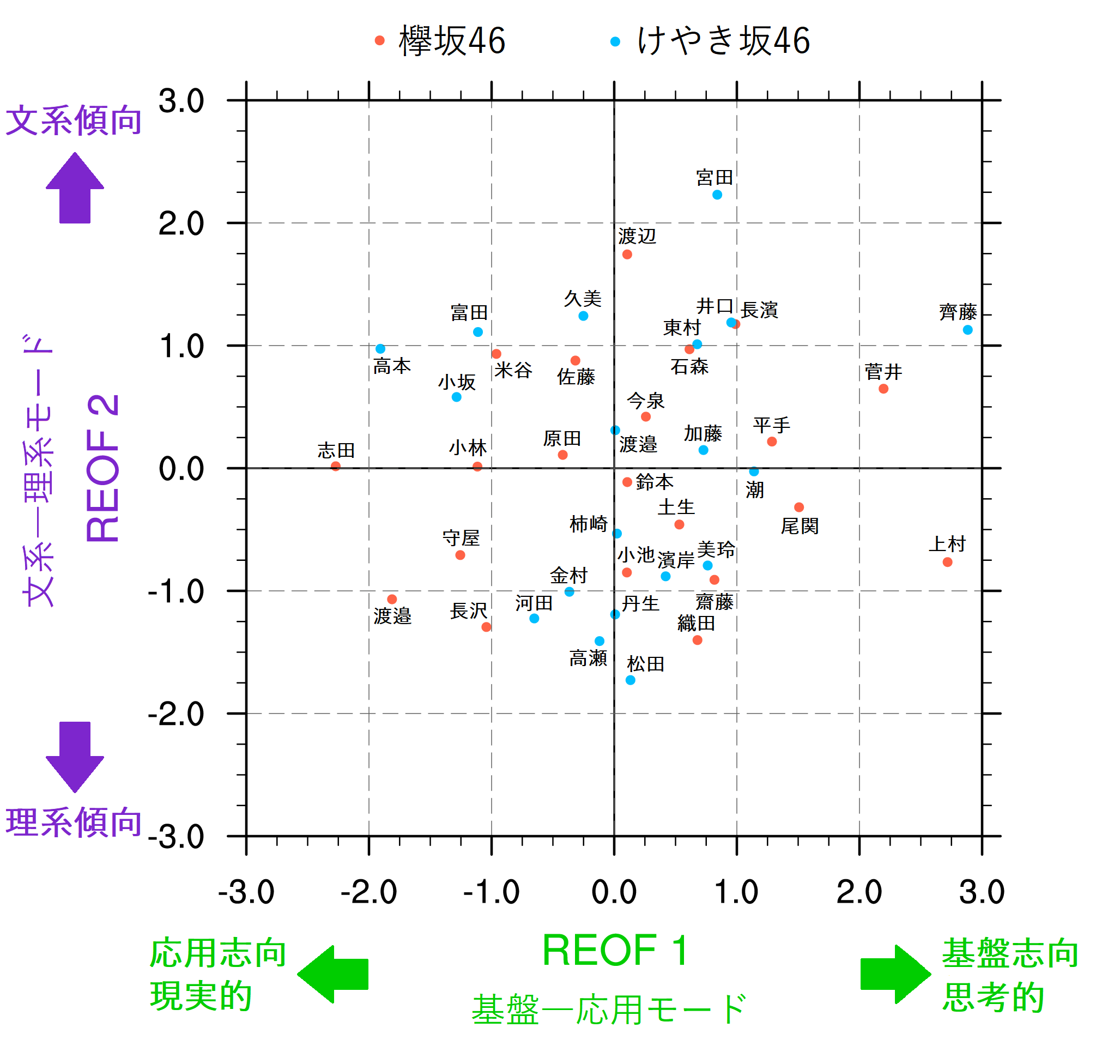
そのようにして得られたパターンが図10であり，これに対応するスコアの散布図が図11である。回転後のモードをREOF1，REOF2と呼ぶことにする。ちなみに，45度回転させるとそれぞれのモードの分散寄与率はちょうど等しくなる(元のEOF1とEOF2の中間である約31％)ため，REOFの後の1や2の数字にもはや意味はない。期待した通り，国語・社会の得点が高く，数学・理科の得点が低い「文系―理系モード」がREOF2として求められた。また，これは欅坂46のみやけやき坂46のみから求まった「文系―理系モード」よりも各教科に一様に点数が分配されているように見える(図2，図5)。REOF1は，国語・数学の得点が高く，社会・理科の得点が低いパターンを示す。REOF1のスコアが高いメンバーは，社会・理科よりも国語・数学が得意で，より思考的あるいは基盤的な教科が得意だと言えるかもしれない。一方で，REOF1のスコアが低いメンバーは，国語・数学よりも社会・理科が得意で，より現実的あるいは応用的な教科が得意だと言えるかもしれない。そこで，ここではこれを「基盤―応用モード」と名付けることにする。もちろん，先に述べたように，REOF1をこのような表現を用いてこのように解釈することを正当化するものはなく，これが本当に適切かどうかは分からない(REOF2についても同様である)。あくまでイメージしやすくするための「あだ名」程度だと思ってほしい。最後に，REOF1とREOF2のそれぞれに対して，上位13名を高指数，下位13名を低指数として全メンバーを9通りに分類したものが以下の表8である。

表8：欅坂/けやき坂46の学力パターン分類

		基盤―応用モード
		応用志向・現実的	バランス型	基盤志向・思考的
文系―理系 モード	文 系 傾 向	米谷奈々未・佐藤詩織 富田鈴花・高本彩花	佐々木久美・渡辺梨加 東村芽依・石森虹花	長濱ねる・宮田愛萌 菅井友香・井口眞緒 齊藤京子
	バ ラ ン ス 型	原田葵・守屋茜 小林由依・小坂菜緒 志田愛佳	渡邉美穂・柿崎芽実 鈴本美愉・土生瑞穂 今泉佑唯	潮紗理菜・尾関梨香 平手友梨奈・加藤史帆
	理 系 傾 向	金村美玖・長沢菜々香 河田陽菜・渡邉理佐	高瀬愛奈・松田好花 丹生明里・小池美波 濱岸ひより	織田奈那・齋藤冬優花 上村莉菜・佐々木美玲